Table of Contents
ELECTRONIC SYSTEMS
Introduction
Electronics can be broadly classified into two types according to the type of signal used in the system. They are:
1. Analog Electronics
2. Digital Electronics
In analog electronics, we study signals (information) that are continuous in nature. Examples of signals which are analog in nature are: rise or fall in temperature, rise or fall in pressure, voice signal/information, picture/video signal/information etc.
A sine wave is another example of an analog signal. In analog circuits, the output voltage/current varies continuously. Because of this, the output voltage/current can have an infinite number of values.
In digital electronics, we have a two-state operation. This means the output can be either high or low. For example, when a LED (Light Emitting Diode) is ON (or glowing) we call it a high state and when it is OFF (not glowing), we call it a low state.
In the binary system, we have two symbols, viz., 0 and 1. In one system called positive logic system, we assign the ON condition of LED as state 1 and the OFF condition of the LED as state 0. (There is another system called a negative logic system. In that system, the ON condition is assigned as state 0 and OFF condition as state 1).
Number System
The technique to represent and work with numbers is called the number system. The most widely used number system is the positional system. In this system, the position of various digits indicates the significance to be attached to that digit. For example, the number 1430.34 can be written as lx103 + 4×102 + 3×101 + 0x10°+ 3×10-1 + 4×10-2.
Hence the position of 103 is called as 1000th position and that of 102 as 100 positions and so on. In the positional number system, we have one term called base or radix.
Base or the radix is a value that indicates how many symbols are used in a particular numbering system.
DECIMAL Number System
In the decimal system, we have ten symbols viz., 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. So we say that the decimal system is having a radix (or base) of 10.
For example, the decimal number 1234 consists of the digit 4 in the unit’s position, 3 in the tens position, 2 in the hundreds position, and 1 in the thousands position.
Its value can be written as
(1 x 1000)+ (2 x 100)+ (3 x 10)+ (4 x l)
=(1 x 103)+ (2 x 102)+ (3 x 101)+ (4 x l00)
=1000 + 200 + 30 + 4=1234
Decimal numbers can be written in the following formats
1234
(1234)10
123410
Binary Number System
The easiest way to vary instructions through electric signals is the two-state system – on and off. On is represented as 1 and off as 0, though 0 is not actually “no signal” but a signal at a lower voltage. The number system having just these two digits – 0 and 1 – is called a binary number system.
Example Binary Number: (11010)2
Bit, Nibble and Byte:
Computer memory is measured in terms of how many bits it can store. Here is a chart for memory capacity conversion.
A Bit is nothing but a single digit (or symbol). In a binary system, it is either 0 or 1.
A Nibble is a group of 4 bits. For example, 1001 is a nibble.
A Byte is a group of 8 bits.
An example for a byte is 1011 1101 is one byte.
1 byte (B) = 8 bits
1 Kilobytes (KB) = 1024 bytes
1 Megabyte (MB) = 1024 KB
1 Gigabyte (GB) = 1024 MB
1 Terabyte (TB) = 1024 GB
1 Petabyte (PB) = 1024 TB
1 Exabyte (EB) = 1024 PB
1 Zettabyte (ZB) = 1024 EB
1 Yottabyte (YB) = 1024 ZB
Conversion of binary to decimal ( base 2 to base 10)
Example 1: Find the decimal equivalent of (11010)2
110102 = 1×24 + 1×23 + 0×22 + 1×21 + 0×20
= 16 + 8 + 0 + 2 + 0
= (26)10
Example 2: convert (1000100)2 to decimal
(1000100)2 = 64 + 0 + 0+ 0 + 4 + 0 + 0 = (68)10
Conversion of decimal to binary (base 10 to base 2)
Example 3: convert (68)10 to binary
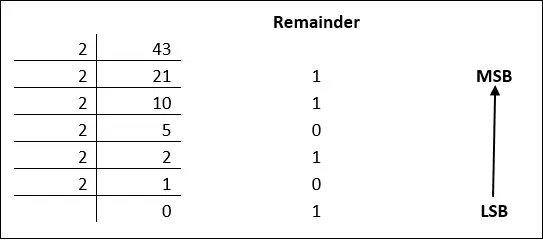
68/¸2 = 34 remainder is 0
34/ 2 = 17 remainder is 0
17 / 2 = 8 remainder is 1
8 / 2 = 4 remainder is 0
4 / 2 = 2 remainder is 0
2 / 2 = 1 remainder is 0
1 / 2 = 0 remainder is 1
Answer =( 1 0 0 0 1 0 0)2
Note: the answer is read from the bottom (MSB) to the top (LSB) as 10001002
Example 4: Convert (43)10 to binary
Conversion of decimal fraction to binary fraction
Instead of division, multiplication by 2 is carried out and the integer part of the result is saved and placed after the decimal point. The fractional part is again multiplied by 2 and the process is repeated.
Example 5:
Convert ( 0.68)10 to a binary fraction.
0.68 x 2 = 1.36 integer part is 1
0.36 x 2 = 0.72 integer part is 0
0.72 x 2 = 1.44 integer part is 1
0.44 x 2 = 0.88 integer part is 0
Answer = 0. 1 0 1 0….. (top to bottom)
Example:
Convert (68.68)10 to binary equivalent.
Do it yourself
The Answer is = 1 0 0 0 1 0 0 . 1 0 1 0….
Octal Number System
The octal number system has eight digits – 0, 1, 2, 3, 4, 5, 6 and 7. An octal number system is also a positional value system in which each digit has its value expressed in powers of 8.
1 octal digit is equivalent to 3 bits.
Conversion of octal to decimal ( base 8 to base 10)
Example 1: convert (632)8 to decimal
= (6 x 82) + (3 x 81) + (2 x 80)
= (6 x 64) + (3 x 8) + (2 x 1)
= 384 + 24 + 2
= 41010
Example 2: convert (726)8 to decimal
7268 = 7×82 + 2×81 + 6×80
= 448 + 16 + 6
= 47010
Conversion of decimal to octal ( base 10 to base 8)
Example: convert (177)10 to octal
177 / 8 = 22 remainder is 1
22 / 8 = 2 remainder is 6
2 / 8 = 0 remainder is 2
Answer = (2 6 1)8
Note: the answer is read from bottom to top as (261)8, the same as with the binary case.
Example: convert (473)10 to octal

47310 = 7318
Conversion of a decimal fraction to an octal fraction is carried out in the same manner as a decimal to binary except that now the multiplication is carried out by 8.
Conversion of binary to Octal and Vice Versa
To convert a binary number to an octal number, these steps are followed
Starting from the least significant bit (LSB), make groups of three bits. If there are one or two bits less in making the groups, 0s can be added after the most significant bit. Convert each group into its equivalent octal number
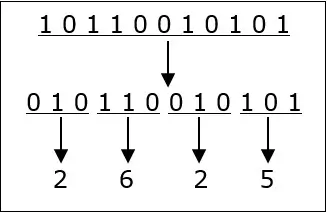
(10110010101)2= (2625)8
To convert an octal number to binary, each octal digit is converted to its 3-bit binary equivalent according to this table.

For example, 546738 = 1011001101110112
Hexadecimal Number System
It has 16 symbols – 0 to 9 and A to F where A is equal to 10, B is equal to 11 and so on till F. Hexadecimal number system is also a positional value system where each digit has its value expressed in powers of 16
Base or radix 16 number system.
1 hex digit is equivalent to 4 bits.
160 = 1, 161 = 16, 162 = 256, 163 = 4096, 164 =65536, …
Conversion of hex to decimal ( base 16 to base 10)
Example: convert (F4C)16 to decimal
(F4C)16 = (F x 162) + (4 x 161) + (C x 160)
= (15 x 256) + (4 x 16) + (12 x 1)
= 3840 + 64 + 12 + 0= (3916)10
Conversion of decimal to hex ( base 10 to base 16)
Example: convert (4768)10 to hex.
= 4768 / 16 = 298 remainder 0
= 298 / 16 = 18 remainder 10 (A)
= 18 / 16 = 1 remainder 2
= 1 / 16 = 0 remainder 1
Answer: (1 2 A 0)16
Note: the answer is read from bottom to top, same as with the binary case.
Conversion of binary to octal and hex
Conversion of binary numbers to octal and hex simply requires grouping bits in the binary numbers into groups of three bits for conversion to octal and groups of four bits for hex conversion.
Groups are formed beginning with the LSB and progressing to the MSB.
Thus, 11 100 1112 = 3478 (Binary to Octal)
11 100 010 101 010 010 0012 = 30252218 (Binary to Octal)
1110 01112 = E716 (Binary to Hex)
1 1000 1010 1000 01112 = 18A8716 (Binary to Hex)
Number System Relationship
We request you to remember the table below to quickly answer the objective-type questions.
Table 1: Decimal, Binary, Octal, and Hex Numbers

Binary arithmetic
Binary Addition
Table 2 is the binary addition table. The entry for 1+1 is 10 which indicates a carry of 1
Table 2: Binary Addition Table
|
+ |
0 |
1 |
|---|---|---|
|
0 |
0 |
1 |
|
1 |
1 |
10 |
Examples
Find the sum of 1011+100, 1101+1001

Binary Subtraction
Uses the same principle of “borrowing” that decimal subtraction uses.
Table 3: Binary Subtraction Table
|
− |
0 |
1 |
|---|---|---|
|
0 |
0 |
1 (with a borrow from the next column) |
|
1 |
1 |
0 |
Example

Note: This problem in decimal is 20 – 9 = 11 which is the answer we get in binary.
Octal Arithmetic
Octal Addition

Examples

Octal Subtraction
This is performed exactly like binary and decimal subtraction with the borrowing technique. Whenever the subtrahend is larger than the minuend, a 1 is borrowed from the next column.
Example:

HEXADECIMAL ARITHMETIC
Hexadecimal Addition
Table 5: Hexadecimal Addition Table

Examples

Hexadecimal Subtraction
Uses the same principle of “borrowing” that decimal and binary subtraction uses.
Example

NEGATIVE NUMBERS
Since you are most familiar with the decimal number system, the question might arise if you can perform subtraction via addition using the complementation technique. The answer is yes, but with the decimal number system, you use a nine’s complement. Let’s check, what is nine’s compliment?
Nine’s Complement
The nine’s complement of a number is found by subtracting the number from a number that consists of all 9’s. The technique is illustrated below.
Forming the 9’s complement
Given 36510 , it’s nine’s complement is: 999 – 365 = 63410
Given 3410 , it’s nine’s complement is: 99 – 34 = 6510
Subtraction as an Addition Operation
 When the larger number is subtracted from the smaller number, no end-around carry will result, but the answer will be in nine’s complement form and of the opposite sign.
When the larger number is subtracted from the smaller number, no end-around carry will result, but the answer will be in nine’s complement form and of the opposite sign.

Sign Magnitude (Binary number)
Several alternative conventions can be used to represent negative (as well as positive) integers, all of which involve treating the MSB as a sign bit. Typically, if the MSB is 0, the number is positive; if the MSB is 1, the number is negative. The simplest form of representation that employs a sign bit is the sign-magnitude representation. In an n-bit word, the right-most n-1 bits represent the magnitude of the integer, and the left-most bit represents the sign of the integer.
For example, in an 8-bit word, the value of +2410 is represented by: 000110002, while the value of –2410 is represented by 100110002.
There are several disadvantages to sign-magnitude representation. One is that addition and subtraction operations require a consideration of both the signs of the numbers and their relative magnitudes to carry out the required operation.
Another disadvantage is that there are two representations of 0. Using an 8-bit word, both 000000002 and 100000002 represent 0 (the first +0, the latter –0). This makes logical testing for equality on 0 more complex (two values need to be tested). Because of these disadvantages, sign-magnitude representation is rarely used in implementing the integer portion of the ALU.
Two’s Complement
Like sign-magnitude, two’s complement uses the MSB as a sign bit, thus making it easy to test if an integer is positive or negative. Two’s complement differs from sign-magnitude in the way the remaining n-1 bits (of an n-bit word) are interpreted.
Two’s complement representation has only a single representation for the value of 0. The two’s complement of a binary number is found by subtracting each bit of the number from 1 and adding 1.
Example 1

Thus 011 is the twos complement of 101 or the representation of –5.
Example 2
10 – 6 = 4 in base 10
1010 – 110 = 100 in base 2
The two’s complement of 6 is 1010 over four bits
1010 + 1010 = 10100 since we are working with 4-bit numbers the MSB is discarded and we are left with 0100 where the MSB is 0 leaving a value of 100 which is the binary representation of (4)10.
An alternate way of performing a two’s complementation (which does exactly the same thing the addition does without thinking about doing the subtraction and the addition) is as follows: beginning with the LSB and progressing toward the MSB, leave all 0 bits unchanged and the first 1 bit unchanged, after encountering the first 1 bit, complement all remaining bits until the MSB has been processed. The resulting number is the two’s complement of the original number.
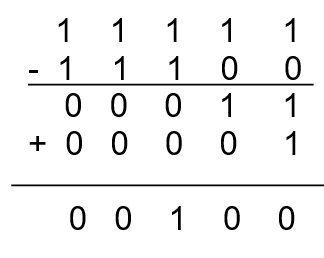
Example 3:
Consider the number 111002 (this is 2810) The two’s complement is: 001002 achieved by:

Note that we get the same answer if we use the original technique.
This is a 30 Page Preview. To continue reading, purchase the remaining content


